题解 P5663 【加工零件【民间数据】】
kradcigam
2019-11-23 18:14:21
# [博客园体验更佳](https://www.cnblogs.com/zhaohaikun/p/12180821.html)
## 讲讲我的做法
### 确定做法
首先,看到这道题,我直接想到的是递归,于是复杂度就上天了,考虑**最短路**。
### 如何用最短路
首先,看一张图
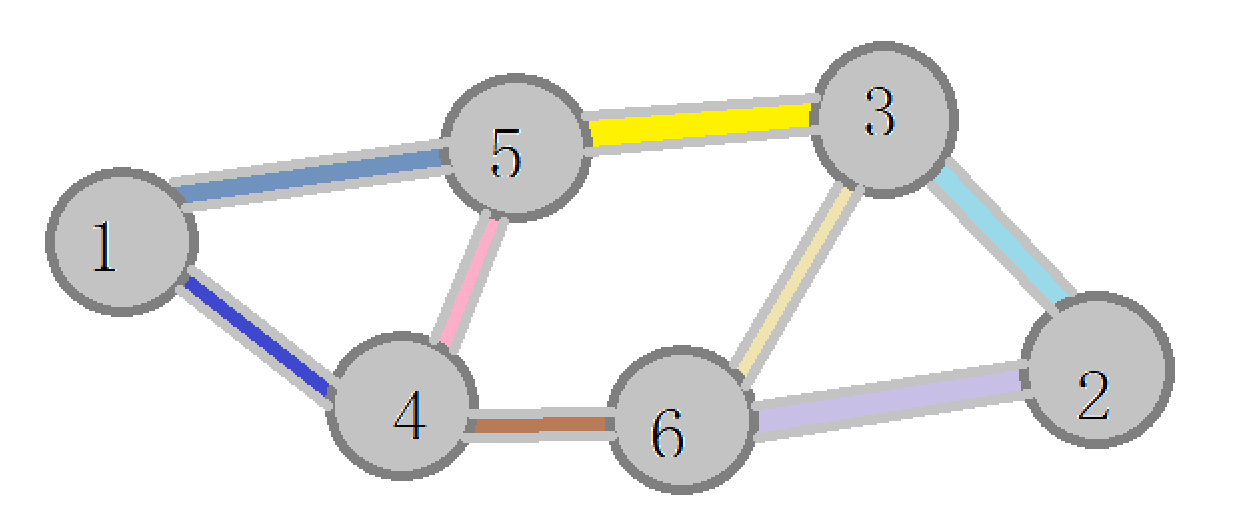
我们该如何解决问题?
> 问题:$3$做$5$阶段的零件$1$要不要做呢?
其实,实质就是看$3$到$1$有没有长度为$5$的路径。
> 问题:$3$做$7$阶段的零件$1$要不要做呢?
其实,实质就是看$3$到$1$有没有长度为$7$的路径。
> 问题:$3$做$6$阶段的零件$1$要不要做呢?
其实,实质就是看$3$到$1$有没有长度为$6$的路径。
仔细思考这$3$个问题,我们会发现,**如果$3$到$1$有长度为$5$的路径,那么$3$到$1$一定有长度为$7$的路径,但并不一定有长度为$6$的路径。**
所以,我们要对每个点求一遍奇数路径,和偶数路径。
### 实现最短路
最短路的算法有很多,这道题最好用$dijkstra$,或$bfs$。
这道题的时限并不紧,并且$dijkstra$**细节太多**,我就来演示$bfs$实现的最短路
```cpp
void bfw(){//我有一个好朋友叫bfw,所以我写bfs时,喜欢把函数名起为bfw
memset(ji,0x3f,sizeof(ji));//奇数最短路径
memset(ou,0x3f,sizeof(ou));//偶数最短路径
queue<pair<int,int> >q;
q.push(make_pair(1,0));
ou[1]=0;
while(q.size()){
int x=q.front().first,y=q.front().second;
for(int i=0;i<v[x].size();i++){
if(y%2==1){//奇数+1=偶数
if(y+1<ou[v[x][i]]){
ou[v[x][i]]=y+1;//更新答案
q.push(make_pair(v[x][i],y+1));
}
}else{//偶数+1=奇数
if(y+1<ji[v[x][i]]){
ji[v[x][i]]=y+1;//更新答案
q.push(make_pair(v[x][i],y+1));
}
}
}
q.pop();
}
}
```
$v$数组是一个动态数组,也就是$vector$,曹老师教我们**多用$STL$写程序**
如果你写这样的$bfs$民间数据会$WA$ $1$个点 ,这个点是这样的
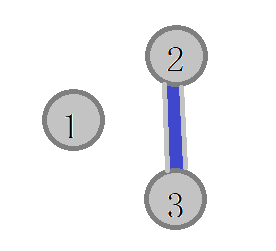
$1$号点是一个孤点,没有偶数路径,所以,我们的$bfs$要这么写
```cpp
void bfw(){//我有一个好朋友叫bfw,所以我写bfs时,喜欢把函数名起为bfw
memset(ji,0x3f,sizeof(ji));//奇数最短路径
memset(ou,0x3f,sizeof(ou));//偶数最短路径
queue<pair<int,int> >q;
for(int i=0;i<v[1].size();i++){
ji[v[1][i]]=1;
q.push(make_pair(v[1][i],1));
}
while(q.size()){
int x=q.front().first,y=q.front().second;
for(int i=0;i<v[x].size();i++){
if(y%2==1){//奇数+1=偶数
if(y+1<ou[v[x][i]]){
ou[v[x][i]]=y+1;//更新答案
q.push(make_pair(v[x][i],y+1));
}
}else{//偶数+1=奇数
if(y+1<ji[v[x][i]]){
ji[v[x][i]]=y+1;//更新答案
q.push(make_pair(v[x][i],y+1));
}
}
}
q.pop();
}
}
```
### 简要讲解主程序
有了这些主程序应该是很简单的了
```cpp
int main(){
int n,m,q;
read(n);read(m);read(q);
for(int i=1;i<=m;i++){
int x,y;
read(x);read(y);//无向边
v[x].push_back(y);//连边
v[y].push_back(x);//连边
}
bfw();//跑最短路
while(q--){
int x,y;
read(x);read(y);
if(y%2==0){
if(ou[x]>y)puts("No");//如果大于就不可能了
else puts("Yes");
}else{
if(ji[x]>y)puts("No");//如果大于就不可能了
else puts("Yes");
}
}
return 0;
}
```
### 总结
先来看一看这题完整的代码了
```cpp
#include <bits/stdc++.h>
using namespace std;
template<typename T>inline void read(T &FF){
T RR=1;FF=0;char CH=getchar();
for(;!isdigit(CH);CH=getchar())if(CH=='-')RR=-1;
for(;isdigit(CH);CH=getchar())FF=(FF<<1)+(FF<<3)+(CH^48);
FF*=RR;
}
template<typename T>void write(T x){
if(x<0)putchar('-'),x*=-1;
if(x>9)write(x/10);
putchar(x%10+48);
}
vector<int>v[100010];
int ji[100010],ou[100010];
void bfw(){//我有一个好朋友叫bfw,所以我写bfs时,喜欢把函数名起为bfw
memset(ji,0x3f,sizeof(ji));//奇数最短路径
memset(ou,0x3f,sizeof(ou));//偶数最短路径
queue<pair<int,int> >q;
for(int i=0;i<v[1].size();i++){
ji[v[1][i]]=1;
q.push(make_pair(v[1][i],1));
}
while(q.size()){
int x=q.front().first,y=q.front().second;
for(int i=0;i<v[x].size();i++){
if(y%2==1){//奇数+1=偶数
if(y+1<ou[v[x][i]]){
ou[v[x][i]]=y+1;//更新答案
q.push(make_pair(v[x][i],y+1));
}
}else{//偶数+1=奇数
if(y+1<ji[v[x][i]]){
ji[v[x][i]]=y+1;//更新答案
q.push(make_pair(v[x][i],y+1));
}
}
}
q.pop();
}
}
int main(){
int n,m,q;
read(n);read(m);read(q);
for(int i=1;i<=m;i++){
int x,y;
read(x);read(y);//无向边
v[x].push_back(y);//连边
v[y].push_back(x);//连边
}
bfw();//跑最短路
while(q--){
int x,y;
read(x);read(y);
if(y%2==0){
if(ou[x]>y)puts("No");//如果大于就不可能了
else puts("Yes");
}else{
if(ji[x]>y)puts("No");//如果大于就不可能了
else puts("Yes");
}
}
return 0;
}
```
这道题还是比较有**思维含量**的,民间数据也出的很好,让我们思考全面。
最后,还是希望大家不懂就在评论区问,觉得好就点赞!